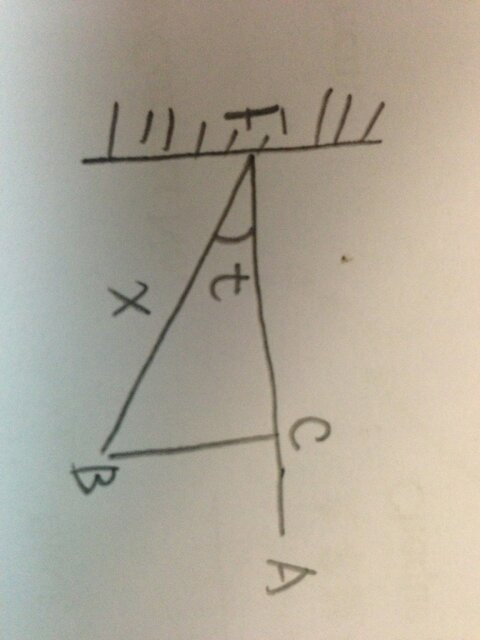Offset LNBs: Theory & Practice

[MJFlash]

Hi, Anole!

Many thanks for the excellent advice - I've revised the first post to include west/east, and have posted in both of the threads you mentioned (at least I think I posted in the right threads ). Thanks again!

Best Wishes!
Mark

 

[MJFlash]

Hi, Guys!

If other folks try this out, please post your results here! If indeed this formula works out well enough, an interesting possibility comes up: you could reverse the formula as a means of measuring the focal length of any unknown dish. You'd want to be careful to measure accurately, but it's a cool way to figure out what that old dish sitting in the backyard is actually all about!

Have Fun!

 

[GenBap]

Sorry to bring up an old thread but do these calculations really work?

 

[Anole]

Like anything here on the forum... if you follow instructions, it just works.

Scan through this thread looking for the pictures. You'll see quickly.
Linuxman and entire arc on 6' Prodelin:
http://www.satelliteguys.us/free-ai...st-way-receive-whole-ku-arc-fixed-dishes.html

 

[chuliu]

Hi MJFlash,
May I ask how you derived the formula?
Here in my country we use a different formula for multi lnb position:
Horizontal offset = focal_length * tan(dish_azimuth - new_azimuth)
Vertical offset = focal_length * tan(dish_elevation - new_elevation)

As an example, your satellite dish is a Fortec Star 90cm, which has a focal length of 510mm. The offsets for you are therefore:

Horizontal: 510mm * tan(174.9 - 160.5 [degrees]) = 130 mm
Vertical: 510mm * sin(46.5 - 44.8 [degrees]) = 15.13 mm

At small angle, my approach is close to yours.
But at larger angle, like 30-40 degrees, the difference becomes larger.
Where I come from, we use 180cm dish to receive satellite in the range of 110E, 113E, 124E, 128E, the azimuth difference is in the range of 5-45 degrees,
where the difference between the two formulas in question is large.

As I got the formula from my fellow sat fan here, and I have not got the chance to really verify it using lnb and dish.
What I did was to mathematically prove my formula, and here it goes,

Assume the dish is a parabolic mirror with focal length of f, further assuming the two satellites are A and B and the azimuth difference is t degree between them.
Remember the Gauss formula for geometric optics, 1/p + 1/q = 1/f where p is the distance between object and the mirror, q the distance between the image and the mirror,
and f the focal length and also the magnify factor=q/p

Next, let's draw a pic of A,B, and the parabolic mirror F
Let the distance between A and F be X
Then the length of sub point C of B on line AF line BC=x sin t
and the length of FC=x cos t






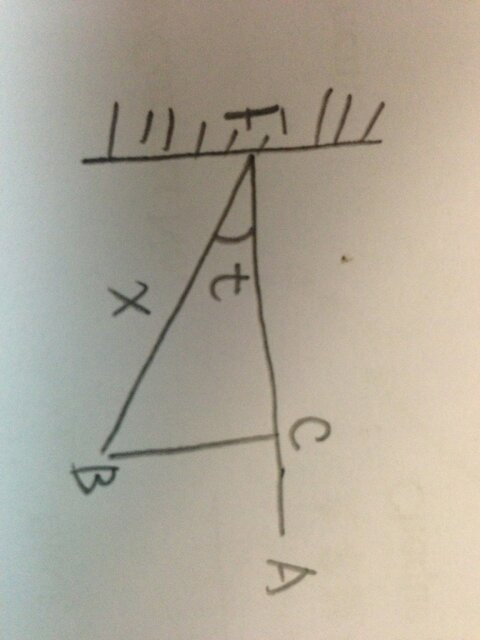
Now let's plug the number to the Gauss formula
since 1/BF ? 1/q = 1/f
since BF is very large, 1/BF can be ignored,
q=f
M=q/p=f/p=f/FC=f/(x cos t)
so we have the final formula:
the image of B is at B' whose position relative to the focal point =
M*p=f/(x cos t) * x sin t
=f tan t

I am here to verify the correctness of my proof and so the correctness of the formula regarding the position of the second lnb to the original lnb.

Thanks.

 

[wallyhts]

Welcome to satguys great post.