A few months ago I found interesting article by John Legon, mostly known as a mathematician researching Egyptian Pyramids.
John also is involved in satellite reception and devised some equations for finding parameters of unknown dishes.
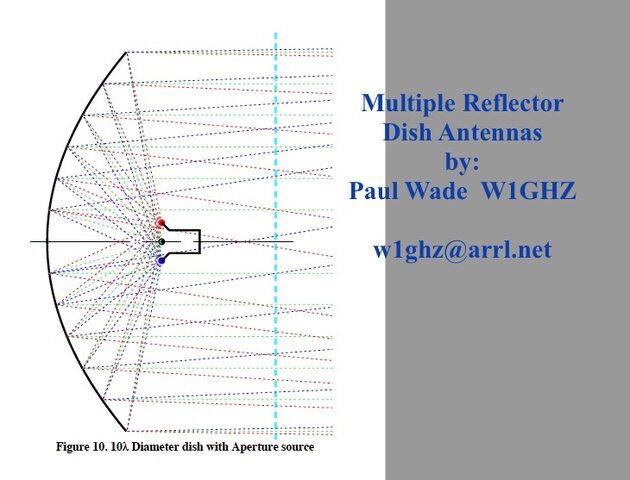
I took a screenshot of part of his article.
What is puzzling for me is his statement that the left and right sides of a dish whose top and bottom were "truncated" for
making its shape more "modern" - that these sides enhance the dish's selectivity for receiving adjacent satellites.
I think that the only factor which determines the angle of a cone what the dish "sees" - is its focal length.
If the dish's focal length is relatively long, it will "see" just one bird. If its focal length is short, it will be vulnerable to adjacent satellites.
I am curious what other Members think about it?

John also is involved in satellite reception and devised some equations for finding parameters of unknown dishes.
I took a screenshot of part of his article.
What is puzzling for me is his statement that the left and right sides of a dish whose top and bottom were "truncated" for
making its shape more "modern" - that these sides enhance the dish's selectivity for receiving adjacent satellites.
I think that the only factor which determines the angle of a cone what the dish "sees" - is its focal length.
If the dish's focal length is relatively long, it will "see" just one bird. If its focal length is short, it will be vulnerable to adjacent satellites.
I am curious what other Members think about it?